Theorem 1.1.8: Complex Numbers are a Field |
The set of complex numbers C with addition and multiplication as
defined above is a field with additive and multiplicative identities
(0,0) and (1,0). It extends the real numbers
R via the isomorphism (x,0) = x.
We define the complex number i = (0,1). With that definition
we can write every complex number interchangebly as
z = (x,y) = x + i*y = x + i y
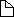 Back
Back
|
We need to prove the field axioms for our definition of addition and
multiplication:
- z + w = (x,y) + (u,v) = (x+u, y+v)
- z * w = (x,y) * (u,v) = (x*u - y*v, x*v + y*u)
1. Both + and * are associative, which is obvious
for addition. For multiplication we nned to show that a*(b*c)=(a*b)*c.
Let
a=(x1,y1),
b=(x2,y2), and
c=(x3,y3). Then:
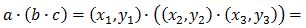
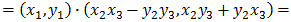
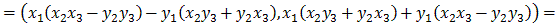
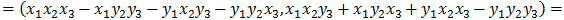
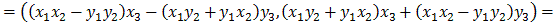
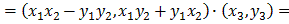
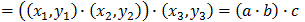
2. Both + and * are commutative, i.e.
a+b=b+a and a*b=b*a
Exercise
3. The distributive law holds, i.e. a*(b+c)=(a*b)+(a*c)
Exercise
4. The additive identity is (0,0), and the multiplicative
identity is (1,0), which you can easily confirm.
5. The additive inverse to (x,y) is (-x,-y). The
multiplicative inverse to (x,y) is
(x/(x2+y2), -y/(x2+y2).
That shows that C is a field.
We now identify the real number x with the complex number
(x,0). Thus, the (real) numbers 0 and 1 are the same as the
complex numbers (0,0) and (1,0), respectively.
Technically, the map
f: R 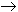 {(x,y)
{(x,y) 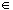 C: y = 0}
C: y = 0}
defined via f(x)=(x,0) is an isomorphism (a bijection such that it
and its inverse are homomorphisms) that identifies the real numbers with a subset
of the complex numbers.
The complex number (0,1) has the property that
(0,1)*(0,1)=(-1,0), which is the same property as our symbol
i.
Interactive Complex Analysis, ver. 1.0.0
(c) 2006-2007, Bert G. Wachsmuth
Page last modified: May 29, 2007
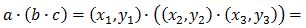
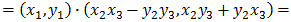
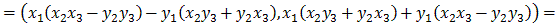
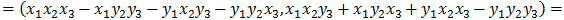
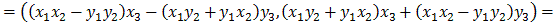
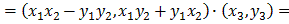
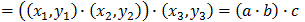
 {(x,y)
{(x,y)  C: y = 0}
C: y = 0}