5.2. Compact and Perfect Sets
Why these ads ...
We have already seen that all open sets in the real line can be written as the countable
union of disjoint open intervals. We will now take a closer look at closed sets. The most
important type of closed sets in the real line are called compact sets:
| Definition 5.2.1: Compact Sets |
| |
A set S of real numbers is called compact if every sequence in S
has a subsequence that converges to an element again contained in S.
|
| Examples 5.2.2: |
| |
 Is the interval [0,1] compact ? How about [0, 1) ?
Is the interval [0,1] compact ? How about [0, 1) ?
 Is the set {1, 2, 3} compact ? How about the set N of natural numbers ?
Is the set {1, 2, 3} compact ? How about the set N of natural numbers ?
 Is the set {1, 1/2, 1/3, 1/4, ...} compact ?
Is the set {1, 1/2, 1/3, 1/4, ...} compact ?
 Is the set {1, 1/2, 1/3, 1/4, ...}
Is the set {1, 1/2, 1/3, 1/4, ...}  {0} compact ? {0} compact ?
|
It is not easy to see what compact sets really look like, based on this definition. However,
the following result gives a nice characterization of them, and lets you answer the above
questions easily.
The above definition of compact sets using sequence can not be used in more abstract
situations. We would also like a characterization of compact sets based entirely on open
sets. We need some definitions first.
| Definition 5.2.4: Open Cover |
| |
Let S be a set of real numbers. An open cover of S is a collection
C of open sets such that S 
 C. The collection C of open sets is
said to cover the set S. C. The collection C of open sets is
said to cover the set S.
A subset of sets from the collection C that still covers the set S is
called a subcovering of S.
|
| Examples 5.2.5: |
| |
 Let S = [0, 1], and C = { (-1/2, 1/2), (1/3, 2/3), (1/2, 3/2)}.
Is C an open cover for S ?
Let S = [0, 1], and C = { (-1/2, 1/2), (1/3, 2/3), (1/2, 3/2)}.
Is C an open cover for S ?
 Let S = [0, 1]. Define
Let S = [0, 1]. Define 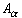 =
{ t =
{ t  R : | t - R : | t - 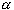 |
< |
<  and and 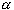
 S} for a fixed S} for a fixed
 > 0. Is the collection of all
{ > 0. Is the collection of all
{ 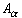 }, }, 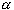
 S, an open cover for S ? How many
sets of type S, an open cover for S ? How many
sets of type 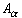 are actually needed to cover S ? are actually needed to cover S ?
 Let S = (0, 1). Define a collection C = { (1/j, 1), for all j > 0 }.
Is C an open cover for S ? How many sets from the collection C are
actually needed to cover S ?
Let S = (0, 1). Define a collection C = { (1/j, 1), for all j > 0 }.
Is C an open cover for S ? How many sets from the collection C are
actually needed to cover S ?
|
Here is the characterization of compact sets based only on open sets:
Compact sets share many properties with finite sets. For example, if
A and
B are two non-empty sets with
A  B
B then
A  B
B #
0. That is,
in fact, true for finitely many sets as well, but fails to be true for infinitely
many sets.
| Examples 5.2.7: |
| |
 Consider the collection of sets (0, 1/j) for all j > 0. What is the intersection
of all of these sets ?
Consider the collection of sets (0, 1/j) for all j > 0. What is the intersection
of all of these sets ?
 Can you
find infinitely many closed sets such that their intersection is empty and such that
each set is contained in its predecessor ? That is, can you find sets
Aj such that
Aj+1 Can you
find infinitely many closed sets such that their intersection is empty and such that
each set is contained in its predecessor ? That is, can you find sets
Aj such that
Aj+1
 Aj and
Aj and
 Aj = 0 ?
Aj = 0 ?
|
Compact sets, on the other hand, have the following nice property, which will be used in
some of the following chapters:
Another interesting collection of closed sets are the perfect sets:
| Example 5.2.10: |
| |
 Find a perfect set. Find a closed set that is not perfect. Find a compact set that
is not perfect. Find an unbounded closed set that is not perfect. Find a closed set
that is neither compact nor perfect.
Find a perfect set. Find a closed set that is not perfect. Find a compact set that
is not perfect. Find an unbounded closed set that is not perfect. Find a closed set
that is neither compact nor perfect.
 Is the
set {1, 1/2, 1/3, ...} perfect ? How about the set {1, 1/2, 1/3, ...} Is the
set {1, 1/2, 1/3, ...} perfect ? How about the set {1, 1/2, 1/3, ...}
 {0} ? {0} ?
|
As an application of the above result, we will see that perfect sets are closed sets that
contain lots of points:
This can yield a quick, but rather sophisticated proof of the fact that the interval [a, b] is
uncountable: the interval [a, b] is a perfect set, hence, it must be uncountable.
Another, rather peculiar example of a closed, compact, and perfect set is the Cantor
set.
| Definition 5.2.12: Cantor Middle Third Set |
| |
Start with the unit interval
S0 = [0, 1]
Remove from that set the middle third and set
S1 = S0 \ (1/3, 2/3)
Remove from that set the two middle thirds and set
S2 = S1 \ { (1/9, 2/9)
 (7/9, 8/9) } (7/9, 8/9) }
Continue in this fashion, where
Sn+1 = Sn \
{ middle thirds of subintervals of
Sn }
Then the Cantor set C is defined as
C =  Sn Sn
|
The Cantor set gives an indication of the complicated structure of closed sets in the real
line. It has the following properties:
| Example 5.2.13: Properties of the Cantor Set |
| |
 Show that the Cantor set is compact (i.e. closed and bounded)
Show that the Cantor set is compact (i.e. closed and bounded)
 Show that the Cantor set is perfect (and hence uncountable)
Show that the Cantor set is perfect (and hence uncountable)
 Show that the Cantor set has length zero, but contains uncountably many points.
Show that the Cantor set has length zero, but contains uncountably many points.
 Show that the Cantor set does not contain any open set
Show that the Cantor set does not contain any open set
|
Think about this set. It seems surprising that
- a set of length zero can contain uncountably many points.
- a perfect set does not have to contain an open set
Therefore, the Cantor set shows that closed subsets of the real line can be more
complicated than intuition might at first suggest. It is in fact often used to construct
difficult, counter-intuitive objects in analysis.

 C. The collection C of open sets is
said to cover the set S.
C. The collection C of open sets is
said to cover the set S.
 B then A
B then A  B # 0. That is,
in fact, true for finitely many sets as well, but fails to be true for infinitely
many sets.
B # 0. That is,
in fact, true for finitely many sets as well, but fails to be true for infinitely
many sets.
 Aj. Then A =
Aj. Then A =
 Aj
is not empty.
Aj
is not empty.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  =
{ t
=
{ t  R : | t -
R : | t - 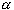 |
<
|
<  and
and