Examples 5.2.5(b):
Let S = [0, 1]. Define
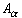 =
{ t
=
{ t  R :
| t -
R :
| t - 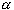 | <
| <
 and
and
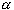
 S}
for a fixed
S}
for a fixed  > 0.
Is the collection of all
{
> 0.
Is the collection of all
{ 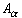 },
},
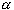
 S,
an open cover for S ? How many sets of type
S,
an open cover for S ? How many sets of type
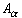 are actually needed to cover S ?
are actually needed to cover S ?
First, each set
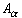 =
{ t
=
{ t  R :
| t -
R :
| t - 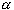 | <
| <
 and
and
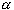
 S}
for a fixed
S}
for a fixed  > 0.
Is the collection of all
{
> 0.
Is the collection of all
{ 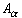 },
},
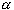
 S,
an open cover for S ? How many sets of type
S,
an open cover for S ? How many sets of type
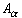 are actually needed to cover S ?
are actually needed to cover S ?
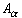 is an open set, because it is the same as an interval around
is an open set, because it is the same as an interval around
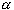 of length
2
of length
2  .
Second, the union of all sets
.
Second, the union of all sets
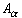 equals the open interval
(-
equals the open interval
(-  ,
1 +
,
1 +  ),
so it contains the set S. Therefore, the collection
{
),
so it contains the set S. Therefore, the collection
{ 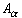 },
},
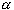
 S
is an open cover of S.
S
is an open cover of S.
The collection
{ 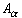 },
},
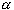
 S
consists of uncountable many sets. In order to cover S,
however, we need only a finite subcollection for any given
S
consists of uncountable many sets. In order to cover S,
however, we need only a finite subcollection for any given
 .
To see this, fix an
.
To see this, fix an
 > 0.
Then let N be the smallest integer greater than
1 /
> 0.
Then let N be the smallest integer greater than
1 /  ,
and define
,
and define
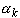 =
k *
=
k *  , k = 0, 1, 2, ... N
, k = 0, 1, 2, ... N
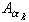 },
k = 0, 1, 2, ..., N
is a covering of S. That is, this new collection forms a
finite subcover of S with respect to the original collection
of sets.
},
k = 0, 1, 2, ..., N
is a covering of S. That is, this new collection forms a
finite subcover of S with respect to the original collection
of sets.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of