Proposition 5.2.8: Intersection of Nested Compact Sets
Suppose
{ Aj } is a collection of sets such that each
Ak is non-empty, compact, and
Aj+1
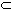 Aj.
Then
A =
Aj.
Then
A = 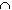 Aj
is not empty.
Aj
is not empty.
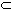 Aj.
Then
A =
Aj.
Then
A = 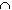 Aj
is not empty.
Aj
is not empty.
Proof:
Each Aj is compact, hence closed and bounded. Therefore, A is closed and bounded as well, and hence A is compact. Pick an aj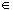 Aj
for each j.
Aj
for each j.
Then the sequence { aj } is contained in A1. Since that set is compact, there exists a convergent subsequence { ajk } with limit in A1.
But that subsequence, except the first number, is also contained in A2. Since A2 is compact, the limit must be contained in A2.
Continuing in this fashion, we see that the limit must be contained in every Aj, and hence it is also contained in their intersection A. But then A can not be empty.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of