Examples 7.1.20(c):
Show that if one starts with an integrable function f
in the Fundamental Theorem of Calculus that is not continuous, the
corresponding function F may not be differentiable.
Our Fundamental Theorem states that if we start with a continuous
function f(t) over some interval [a, b] then
the new function F(x) obtained by integrating f
from a to some variable value x is differentiable:
F(x) =Now let's start with a simple step function that is integrable but not continuous over the interval, say, [-1, 1]. Definef(t) dt is differentiable as long as f is continuous
Then for if x < 0 we have: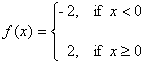
and for x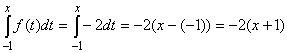
 0
0
But then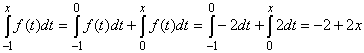
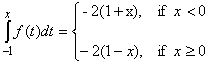
|
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of