Examples 7.1.20(a):
Define a function
F(x) = 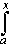 t2 sin(t) dt
for x in the interval [a, a + 10].
t2 sin(t) dt
for x in the interval [a, a + 10].
1.
Since F(x) = 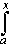 t2 sin(t) dt
for x in the interval [a, a + 10].
t2 sin(t) dt
for x in the interval [a, a + 10].
- Find F(a)
- Find F'(x)
- Find F''(x)
- Find all critical points of F(x) in [a, a + 10]
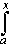 t2 sin(t) dt
the value F(a) is an integral from a to
a. But such an integral is 0 regardless of the integrand.
Therefore F(a) = 0.
t2 sin(t) dt
the value F(a) is an integral from a to
a. But such an integral is 0 regardless of the integrand.
Therefore F(a) = 0.
2. The second part is a direct application of the (second) Fundamental Theorem of Calculus:
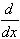
t2 sin(t) dt = x2 sin(x)
3. Since we have computed the first derivative already, it is easy to compute the second derivative:
F''(x) =4. To find the critical points of F we need to find the points where F is not differentiable or where F'(x) = 0. We know that F is differentiable on any closed interval so that the critical points are those whereF'(x) =
x2 sin(x) = 2x sin(x) + x2 cos(x)
F'(x) = x 2 sin(x) = 0Therefore the critical points are x = 0 and x = k
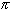 , k=1, 2, ...,
or better those points k = 0, 1, ... that are inside the interval
[a, a+10].
, k=1, 2, ...,
or better those points k = 0, 1, ... that are inside the interval
[a, a+10].
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of