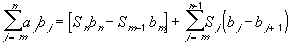Abel Convergence Test
Consider the series 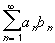 . Suppose that
. Suppose that
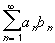 converges.
converges.
This test is rather sophisticated. Its main application is to prove the
Alternating Series test, but one can sometimes use it for other series as
well, if the more obvious tests do not work.
Proof:
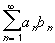 . Suppose that
. Suppose that
- the partial sums
S N =
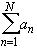 form a bounded sequence
form a bounded sequence
- the sequence
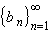 is decreasing
is decreasing
- lim b n = 0
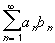 converges.
converges.
First, we need a lemma, called the Summation by Parts Lemma:
Lemma: Summation by Parts
Assuming this lemma is proved, we will use it as follows for Abel's Test:
Consider the two sequences
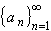 and
and
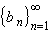 . Let
S N =
. Let
S N =
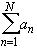 be the
n-th partial sum. Then for any
0
be the
n-th partial sum. Then for any
0  m
m  n
we have:
n
we have:
First, let's assume that the partial sums
S N
are bounded by, say, K. Next, since the sequence
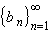 converges to zero, we can choose an integer N such that
| b n | <
converges to zero, we can choose an integer N such that
| b n | <  / 2K.
Using the Summation by Parts lemma, we then have:
/ 2K.
Using the Summation by Parts lemma, we then have:
But the sequence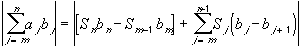
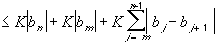
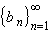 is
decreasing to zero, so in particular all terms must be positive and
all absolute values inside the summation above are superfluous. But then
the sum is a telescoping sum. All that remains is the first
and last term, and we have:
is
decreasing to zero, so in particular all terms must be positive and
all absolute values inside the summation above are superfluous. But then
the sum is a telescoping sum. All that remains is the first
and last term, and we have:
But by our choice of N this is less than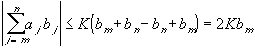
 if we choose n and m larger than the
predetermined N. This proves Abel's Test.
if we choose n and m larger than the
predetermined N. This proves Abel's Test.
What remains to do is the proof of the lemma, which can be found here.

 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 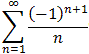 converge or diverge ?
converge or diverge ?
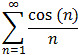 converge or diverge ?
converge or diverge ?