Examples 4.2.18(b):
Note that we can not simply apply the alternating series test, because this series is not alternating. We will rather apply the more sophisticated Abel's test.
To apply Abel's test, we first need to identify two sequences. Let
{ an } = { cos(n) }and
{ b n } = { 1/n }While it is clear that { b n } is decreasing and convergent to zero, it is not clear at all whether the sequence of partial sums of the a n's is bounded or not. We will make an unfair detour here, using some basic formulas from complex analysis:
Recall from Complex Analysis that
cos(t) + i sin(t) = e itfor all real numbers t, where i is the basic complex number given as the square root of -1. Taking this formula for granted, we have:
( cos(1) + i sin(1) ) + ( cos(2) + i sin(2) ) + ... + ( cos(n+1) + i sin(n+1) ) =Therefore, taking absolute values on both sides we can estimate the last expression using the triangle inequality and the fact that | e it | = 1 to obtain:
= e i + e 2i + ... + e (n+1)i =
= e i ( 1 + ( e i ) + ( e i ) 2 + ... + ( e i ) n ) =
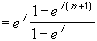
for all n. Finally, using the fact that | a |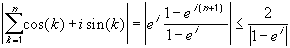
 | a + i b |
for all real numbers a, b, we have
| a + i b |
for all real numbers a, b, we have
Putting the last two expressions together, we see that the sequence of partial sums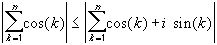
| cos(1) + cos(2) + ... + cos(n) |is bounded for all n. Therefore, both conditions of Abel's test are verified, and hence the original series converges.
Of course, this is an 'unfair' proof, since it uses complex analysis and we have not even defined properly what a complex number is. Therefore, another proof of this example is necessary that uses only real analysis. Such a proof is left as an exercise, as well as the proof that the series does not converge absolutely (not easy).
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 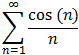 converges conditionally.
converges conditionally.