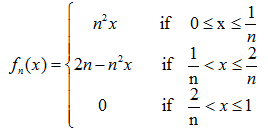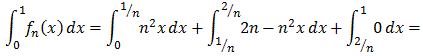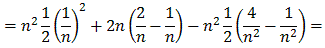Example 8.1.8 (e): Pointwise Convergence does not preserve Integration
Find a pointwise convergent sequence of Riemann-integrable functions whose
limit is Riemann-integrable but
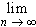
fn(x) dx #
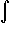
fn(x) dx =
f(x) dx
|
This is perhaps a little tricky, but we could try one of the function sequences we discussed earlier: fn(x) = max(n - n2 |x - 1/n|, 0) where x Each fn is continuous, hence Riemann integrable. The pointwise limit f is zero, which is again integrable. But when we integrate: |
|
for all n. On the other hand, the integral of the limit function is clearly zero so that:
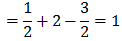
1 =By the way, if we consider the integral as area under a function it is immediately clear from the graph that the fn's integrate to 1 ...
fn(x) dx #
f(x) dx = 0
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  [ 0, 1 ] (you
knew this function would play a bigger role, didn't you). Recall that each
member of this family is piecewise linear, so another way to write
fn is:
[ 0, 1 ] (you
knew this function would play a bigger role, didn't you). Recall that each
member of this family is piecewise linear, so another way to write
fn is: