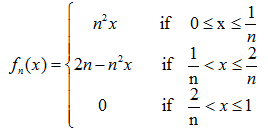Example 8.1.7 (a): Pointwise Convergent Function Sequence
Let fn(x) = max(n - n2 |x - 1/n|, 0),
x  [ 0, 1 ]. Show that
this sequence converges pointwise to the function f(x) = 0
for x
[ 0, 1 ]. Show that
this sequence converges pointwise to the function f(x) = 0
for x  [ 0, 1 ].
[ 0, 1 ].
 [ 0, 1 ]. Show that
this sequence converges pointwise to the function f(x) = 0
for x
[ 0, 1 ]. Show that
this sequence converges pointwise to the function f(x) = 0
for x  [ 0, 1 ].
[ 0, 1 ].
Recall that for each n the function
fn(x) = max(n - n2 |x - 1/n|, 0)
is piecewise linear:
Now take any  > 0. Fix
x > 0. Fix
x  [ 0, 1 ]. [ 0, 1 ].
|
|
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of