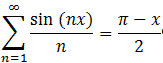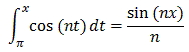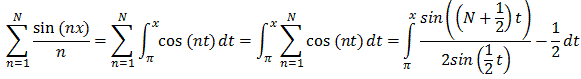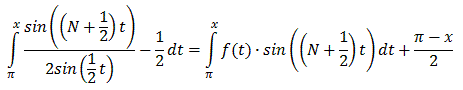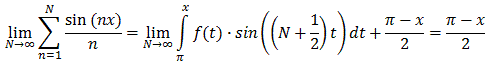Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Example 8.3.2 (b): Function Series Examples

Show that for a fixed x with 0 < x < we have:

This is very interesting: adding up infinitely many "wavy" sine functions is - supposedly - going to be equal to a linear function with slope -1. Indeed, that seems to be correct, as the graphs of two partial sums below show:


The 10-th partial sum
The 100-th partial sum

The proof will be an application of trig identities and a previous integration-by-parts result, but it should be clear how we need to proceed (just as in the geometric series example):

  1. we need to consider the N-th partial sum SN(x) = sin(x) + 1/2 sin(2x) + ... + 1/N sin(Nx)
  2. we need to find a "closed form" for SN(x) that does not involve a summation (or ... dots)
  3. we need to take the limit as N goes to infinity of SN(x), using the closed form to evaluate the limit

The difficult step is the second one, finding a closed form for the partial sums. We will need a technical lemma for that:

Sum of cos Lemma

For x # 2k we have

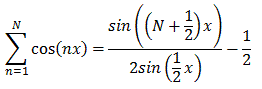
Assuming this lemma to be true, we also need to get 1/n sin(nx) involved. But that is easy:

But then, putting things together:

We can rewrite the integral on the right (and evaluate the last part) to get:

where 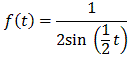is a continously differentiable function. But we have shown previously that

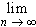
f(x) sin(nx) dx = 0

Therefore:

which is what we wanted to show.

By the way, our statement only applies for 0 < x < 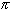. Where in our proof did we use this restriction?

So it remains to prove our technical lemma ...

Next | Previous | Glossary | Map | Discussion