Theorem 6.5.5: Differentiable and Continuity
If f is differentiable at a point c, then f is continuous
at that point c. The converse is not true.
Proof:
Note that
- f(x) - f(c) =
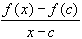 (
x - c )
(
x - c )
As x approaches c, the limit of the quotient exists by assumption and is equal to f'(c), and the limit of the right-hand factor exists also and is zero. Therefore:
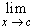 f(x)
- f(c) = 0
f(x)
- f(c) = 0
which is another way of stating that f is continuous at x = c.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of