Interactive Real Analysis - part of MathCS.org

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 6.1. Limits
• 6.2. Continuous Functions
• 6.3. Discontinuous Functions
• 6.4. Topology and Continuity
• 6.5. Differentiable Functions
• 6.6. A Function Primer
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

Theorem 6.5.3: Derivative as Linear Approximation

Why these ads ...

Let f be a function defined on (a, b) and c any number in (a, b). Then f is differentiable at c if and only if there exists a constant M such that

f(x) = f(c) + M ( x - c ) + r(x)

where the remainder function r(x) satisfies the condition

= 0

Context

Proof:

First, suppose f is differentiable at x = c. Let the constant M = f'(c) and set

• r(x) = f(x) - f(c) - f'(c) ( x - c )

We have to check the limit of the quotient

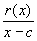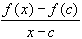• = - f'(c)

Since f is differentiable, the limit of this expression is zero as x approaches c, as required.

Second, suppose that f(x) = f(c) + M ( x - c ) + r(x) for some constant M and 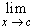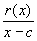= 0 Then

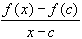• - M =

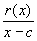
The limit on the right as x approaches c is zero by assumption. Hence, the limit on the left must also be zero, and we recognize the constant M as the derivative of the function f'(c).