Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Weierstrass Function

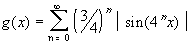
The function g is continuous in R, but not differentiable at any point in R. Incidentally, there are many other functions of this type, and they are best treated in a course on complex analysis.
The graph of the n-th partial sum for Weierstrass's monster. To get a better idea about the limit, try larger values of n (values larger than 30 do not work due to roundoff errors). Try to zoom into the function using the mouse. Can you believe that this function is continuous, but differentiable nowhere ?

Your browser can not handle Java Applets ... Get latest version of Firefox now.
There are many other, similarly constructed. Here is another example which is the same as the function above but without the absolute values:

Your browser can not handle Java Applets ... Get latest version of Netscape now.

Proof:

This function, incidentally, is the one which was used to generate the logo at the title pages. To show that it is continuous, check the entry in the chapter on function sequences and series. To show it is not differentiable will be somewhat more difficult.

We'll do it later ...

Next | Previous | Glossary | Map | Discussion