Definition 6.2.7: Uniform Continuity
A function f with domain D is called uniformly
continuous on the domain D if for any
 > 0 there exists a
> 0 there exists a
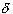 > 0 such that if
s, t
> 0 such that if
s, t  D
and | s - t | <
D
and | s - t | < 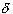 then
| f(s) - f(t) | <
then
| f(s) - f(t) | < 
 > 0 there exists a
> 0 there exists a
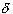 > 0 such that if
s, t
> 0 such that if
s, t  D
and | s - t | <
D
and | s - t | < 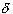 then
| f(s) - f(t) | <
then
| f(s) - f(t) | < 
![]() Take a look at a Java applet illustrating uniform continuity , or
click here for a graphical
explanation and compare this definition to that of 'regular'
continuity.
Take a look at a Java applet illustrating uniform continuity , or
click here for a graphical
explanation and compare this definition to that of 'regular'
continuity.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of