Examples 6.4.7(b):
Does the function 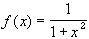 have
an absolute maximum and minimum on [-2, 1] ? How about on the
interval [0,
have
an absolute maximum and minimum on [-2, 1] ? How about on the
interval [0,  )
?
)
?
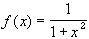 have
an absolute maximum and minimum on [-2, 1] ? How about on the
interval [0,
have
an absolute maximum and minimum on [-2, 1] ? How about on the
interval [0,  )
?
)
?
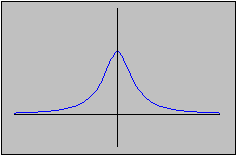
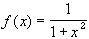
On the other hand, on the unbounded interval [0,  )
the function fails to possess both absolute maximum and minimum.
While 1 is still the absolute maximum, there no longer is an absolute
minimum.
)
the function fails to possess both absolute maximum and minimum.
While 1 is still the absolute maximum, there no longer is an absolute
minimum.
Thus, the boundedness condition in the Max/Min theorem for continuous functions is essential.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of