Interactive Real Analysis
- part of Examples 6.4.2(a):
Let f(x) = x2. Show that f is continuous by proving
Back
- that the inverse image of an open interval is open.
- that the inverse image of a closed interval is closed.
Back
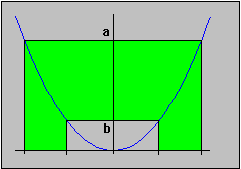
f(x) = x2
- If 0 < a < b then the inverse image of the open interval
(a, b) is
(-
, -
)
(, ).
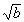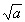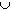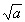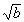In particular, the inverse image is open.
- If a < 0 < b then the inverse image of the open interval
(a, b) is
(-, ),
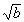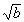which is again open.
- If a < b < 0, then the inverse image of the open interval (a, b) is again open (which set is it ?)
But it is now obvious that the inverse image of closed intervals is again a closed set (note that the empty set is both open and closed).
Hence, we have proved that the function f(x) = x2 is continuous, avoiding the tedious epsilon-delta proof.