Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 6.4.5(a):

If then:
  1. what is the image of [-2, 1] ?
  2. find a closed set whose image is not closed

Note that this function is continuous. The image of the interval [-2, 1] is [1/5, 1]. In particular, the image of a compact set is compact.

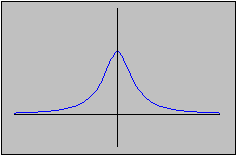
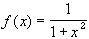
To find a closed set whose image is not closed we must consider an unbounded set. Otherwise, a closed and bounded set is compact, and since the image of a compact set under continuous functions is compact, it is in particular closed again.

But if we look at the closed, unbounded set [0, ), we see that the image of that set under the above function is the set (0, 1], which is not closed.

Next | Previous | Glossary | Map | Discussion