Interactive Real Analysis
- part of Example 6.1.5:
Consider the function f with f(x) = 1 if x is
rational and f(x) = 0 is x is irrational. Does the limit of
f(x) exist at an arbitrary number x ?
Back
Recall that f is called the Dirichlet function. Since f 'jumps
wildly' up and down, we suspect that the function does not have
a limit at any point. This is indeed the case, as is easy to show
using our new definition of limit:
Back
Let c be any real number and pick
= 1/2. Suppose there was a
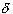> 0 such that whenever
| x - c | < 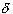then
| f(x) - L | < = 1/2.
We can find a rational number q with
| q - c | < 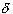. Hence
f(q) = 1, and therefore
| f(q) - L | < 1/2, or | 1 - L | < 1/2or equivalently
| L | > 1/2We can also find an irrational number y with | y - c | <
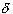. Hence
f(y) = 0, and therefore
| f(y) - L | < 1/2or
| L | < 1/2But that's a contradiction, so the function can not have a limit at any point c.