Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 6.5.2(a):

Find the derivative of f(x) = x and of f(x) = 1 / x
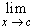
  1. If f(x) = x, then 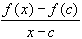= 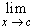(x - c) / (x - c) = 1 so that f'(x) = 1 for all x.
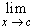
  2. If f(x) = 1 / x, then 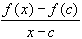= 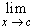(1/x - 1/c) / (x - c) = (c - x) / (x - c) * 1 / (x c) = - 1 / c2, so that f'(x) = - 1 / x2 for all x not equal to zero.
Next | Previous | Glossary | Map | Discussion