Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Examples 6.4.9(a):

Show that the equation cos(x) = x has a solution in the interval [-10, 10].
Let's take a look at the two function f(x) = cos(x) and g(x) = x in one coordinate system: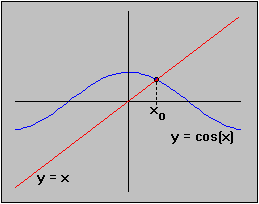
So one can clearly see that there is exactly one solution. We can use Bolzano's theorem to actually prove that there must be at least one solution: Let h(x) = cos(x) - x. Then h is a continuous function and
h(- ) = -1 + > 0
h( ) = -1 - < 0
Hence, by Bolzano's theorem there must be at least one place x0 where h( x0) = 0, or equivalently where cos( x0) = x0.

One can use Bolzano's theorem to construct an algorithm that will find zeros of a function to a prescribed degree of accuracy in many cases. In simple terms:

Would this procedure find the zero of the function f(x) = x2 in the interval [-1, 1] ?

Next | Previous | Glossary | Map | Discussion