6.4. Topology and Continuity
Why these ads ...
While the definition of continuity suffices for functions on the
real line, there are other, more abstract spaces for which this
definition will not work. In particular, our continuity definitions
relies on the presence of an
absolute value. There are
spaces which do not have such a distance function, yet we still
might want to study continuous functions on those abstract spaces.
In this section we will investigate some topological properties
of continuity which will, in fact, apply equally well to more
general settings. In addition, this section will contain several
important theoretical results on continuous function on the real
line.
| Proposition 6.4.1: Continuity and Topology |
| |
Let f be a function with domain D in R. Then
the following statements are equivalent:
- f is continuous
- If D is open, then the inverse image of every open
set under f is again open.
- If D is open, then the inverse image of every open
interval under f is again open.
- If D is closed, then the inverse image of every closed
set under f is again closed.
- If D is closed, then the inverse image of every closed
interval under f is again closed.
- The inverse image of every open set under f is the intersection
of D with an open set.
- The inverse image of every closed set under f is the intersection
of D with a closed set.
Proof
|
This proposition can be used to prove that a function is continuous,
and is especially nice if the domain of the function is either
open or closed. This is true in particular for function defined
on all of
R (which is both open and closed).
| Examples 6.4.2: |
| |
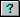 Let f(x) = x2. Show that f is continuous by
proving
Let f(x) = x2. Show that f is continuous by
proving
- that the inverse image of an open interval is open.
- that the inverse image of a closed interval is closed.
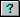 Let f(x) = 1 if x > 0 and f(x) = -1 if x
Let f(x) = 1 if x > 0 and f(x) = -1 if x  0.
Show that f is not continuous by 0.
Show that f is not continuous by
- finding an open set whose inverse image is not open.
- finding a closed set whose inverse image is not closed.
|
Now we know that the inverse images of open sets are open, and
the inverse images of closed sets are closed whenever f is continuous.
What about the images of sets under continuous functions ?
| Examples 6.4.3: |
| |
 Is it true that if f is continuous, then the image of an open set is again
open ? How about the image of a closed set ?
Is it true that if f is continuous, then the image of an open set is again
open ? How about the image of a closed set ?
|
As the above examples show, the image of a closed set is not necessarily
closed for continuous functions. It is also easy to see that the image of
a bounded set is not necessarily bounded. However, the image of bounded
and closed sets under continuous functions is both bounded and closed
again. That is the content of the next theorem.
Since compact sets in the real line are characterized by being
closed and bounded, we should note while it is not true that the
image of a closed set is closed, one must look at an unbounded
closed set for a counterexample. If the set was closed and bounded,
then its image would be closed again, because the image of a compact
set is, in particular, closed, by the above theorem.
| Examples 6.4.5: |
| |
 If
If 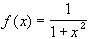 then: then:
- what is the image of [-2, 1] ?
- find a closed set whose image is not closed
 Find examples for the following situations:
Find examples for the following situations:
- A continuous function and a set whose image is not connected.
- A continuous function and a disconnected set whose image is connected.
- A function such that the image of a connected set is disconnected.
- Is it true that inverse images of connected sets under continuous
functions are again connected ?
|
This proposition has several important consequences for continuous functions.
Note that the above example guaranties the existence of an absolute
maximum and minimum, but does not indicate where that maximum
or minimum might occur.
| Examples 6.4.7: |
| |
 Find a continuous function on a bounded interval that is unbounded.
How about a continuous function on a bounded interval that does not have
an absolute maximum but is bounded ?
Find a continuous function on a bounded interval that is unbounded.
How about a continuous function on a bounded interval that does not have
an absolute maximum but is bounded ?
 Does the function
Does the function 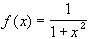 have an absolute maximum
and minimum on [-2, 1] ? How about on the interval
[0, have an absolute maximum
and minimum on [-2, 1] ? How about on the interval
[0, 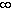 )? )?
|
| Theorem 6.4.8: Bolzano Theorem |
| |
If f is continuous on a closed interval [a, b] and f(a) and
f(b) have opposite signs, then there exits a number c in the
open interval (a, b) such that f(c) = 0.
Proof
|
| Examples 6.4.9: |
| |
 Show that the equation cos(x) = x has a solution in the interval [-10,10].
Show that the equation cos(x) = x has a solution in the interval [-10,10].
 Show that the equation
Show that the equation 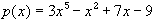 = 0 has at least one
solution in R. = 0 has at least one
solution in R.
|
| Theorem 6.4.10: Intermediate Value Theorem |
| |
If f is continuous on a closed interval [a, b] and d
is any number between f(a) and f(b). Then there exists
a number c in the open interval (a, b) such that f(c) = d.
Proof
|
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  0.
Show that f is not continuous by
0.
Show that f is not continuous by
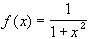 then:
then:
 )?
)?
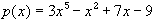 = 0 has at least one
solution in R.
= 0 has at least one
solution in R.