6.1. Limits
Why these ads ...
We now want to combine some of the concepts that we have introduced
before: functions, sequences, and topology. In particular, if
we have some function
f(x) and a given sequence
{ an }, then we can apply the function to each element
of the sequence, resulting in a new sequence. What we would want is that
if the original sequence converges to some number
L, then the new
sequence
{ f( an )} should converge to
f(L),
and if the original sequence diverges, the new one should diverge also.
This seems not too much to ask for, but is quite simple minded.
| Example 6.1.1: |
| |
-
 Consider the function f, where
f(x) = 1 if
x
Consider the function f, where
f(x) = 1 if
x 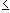 0 and
f(x) = 2 if x > 0. 0 and
f(x) = 2 if x > 0.
- The sequence { 1/n } converges to 0. What happens to the
sequence { f( 1/n ) } ?
- The sequence
{ 3 + (-1)n } is divergent. What happens to the sequence
{ f ( 3 + (-1)n ) } ?
- The sequence
{ (-1)n / n } converges to zero. What happens to the
sequence
{ f ( (-1)n / n ) } ?
|
As the above easy example shows, things can be more complicated
than anticipated. Therefore, we have to attack the problem more
systematically. First, we need to define what we mean by 'limit
of a function'.
| Examples 6.1.3: |
| |
-
 Apply this definition in these cases:
Apply this definition in these cases:
- Let f(x) = m x + b. Then does the limit of that function
exist at an arbitrary point x ?
- Let g(x) = [x], where [x] denotes the greatest
integer less than or equal to x. Then does the limit of g
exist at an integer ? How about at numbers that are not integers ?
- In the above definition, does c have to be in the domain
D of the function ? Is c in the closure(D) ? Do you
know a name for c in terms of topology ?
|
The above definition works quite well to show that a function is not continuous,
because you only have to find one particular sequence whose images do not converge
as a sequence. It is not a good definition, in general, to prove convergence of a
function, because you will have to check every possible convergent sequence,
and that is hard to do. We would therefore like another definition
of convergence or limit of a function.
| Example 6.1.5: |
| |
 Consider the function f with f(x) = 1 if x is
rational and f(x) = 0 if x is irrational. Does the limit of
f(x) exist at an arbitrary number x ?
Consider the function f with f(x) = 1 if x is
rational and f(x) = 0 if x is irrational. Does the limit of
f(x) exist at an arbitrary number x ?
|
Regardless of which of the two definitions might be considered
easier to use in a particular situation, the basic problem right
now is that we have two different definitions for the same concept.
We therefore have to show that both definitions are actually equivalent
to each other.
In other words, both definitions of continuity are equivalent,
and we can use which ever seems the easiest. Here are some basic
properties of limits of functions.
Sometimes a function may not have a limit using the above definitions,
but when the domain of the function is restricted, then a limit
exists. This leads to the concepts of one-sided limits.
| Definition 6.1.8: One-Sided Limits of a Function |
| |
If f is a function with domain D and
c 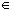 closure(D). Then: closure(D). Then:
- f has a left-hand limit L at c if for
every
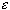 > 0
there exists > 0
there exists
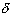 > 0
such that if
x > 0
such that if
x 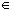 D
and
c - D
and
c - 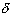 < x < c
then
| f(x) - L | < < x < c
then
| f(x) - L | < 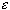 .
We write .
We write
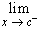 f(x) = L. f(x) = L.
- f has a right-hand limit L at c if for
every
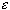 > 0
there exists > 0
there exists
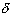 > 0
such that if
x > 0
such that if
x 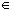 D and
c < x < c + D and
c < x < c +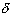 then
| f(x) - L | <
then
| f(x) - L | < 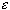 .
We write .
We write
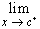 f(x) = L. f(x) = L.
|
This is the formal definition of
x approaching
c either only
from the right side, or only from the left side. These one-sided limits
are related to regular limits in a straight forward manner:
Now that we have some idea about limits of functions, we will
move to the next question: if some sequence converges to
c, and
the function converges to
L as
x approaches
c, then
when is it true that
f(c) = L ? This will be the contents of the next
section, continuity.
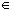 closure (D) if:
given any
closure (D) if:
given any
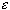 > 0 there exists a
> 0 there exists a
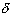 > 0 such that:
> 0 such that:
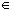 closure(D) then the
following are equivalent:
closure(D) then the
following are equivalent:
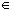 closure(D). Then:
closure(D). Then:
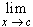 f(x) = L
if and only if
f(x) = L
if and only if
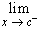 f(x) = L
and
f(x) = L
and
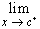 f(x) = L
f(x) = L
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  0 and
f(x) = 2 if x > 0.
0 and
f(x) = 2 if x > 0.