Example 6.1.1:
Consider the function f, where
f(x) = 1 if x 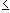 0
and f(x) = 2 if x > 0.
0
and f(x) = 2 if x > 0.
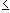 0
and f(x) = 2 if x > 0.
0
and f(x) = 2 if x > 0.
- The sequence {1/n} converges to 0. What happens to the sequence { f( 1/n ) } ?
- The sequence { 3 + (-1)n} is divergent. What happens to the sequence { f(3 + (-1)n)} ?
- The sequence {(-1)n / n } converges to zero. What happens to the sequence { f((-1)n / n ) } ?
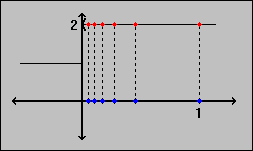
- For the first sequence, we clearly have that f(1/n) = 2 for all n. Hence, the limit of f(1/n) equals 2. So a function applied to a sequence results in a new sequence that can converge to a different number.
- For the second sequence, we know that 3 + (-1)n > 0 for all n. Hence, f(3 + (-1)n) = 2 for all n. This time, a function applied to a divergent sequence results in a convergent one.
- For the third sequence we know that alternating terms switch signs. Hence, f((-1)n / n) = 1 if n is odd, and 2 if n is even. But then the resulting new sequence is divergent. Hence, we have an example where a function can turn a convergent sequence into a divergent one.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of