Interactive Real Analysis
- part of Theorem 5.1.8: Closed Sets, Accumulation Points, and Sequences
- A set S
R
is closed if and only if every Cauchy sequence of elements in
S has a limit that is contained in S.
- Every bounded, infinite subset of R has an accumulation
point.
- If S is closed and bounded, and
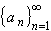is any sequence
in S, then there exists a subsequence
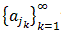of
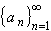that converges
to an element of S.
Context