Proposition 5.3.3: Connected Sets in R are Intervals
Proof:
If S is not an interval, then there exists a, b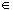 S and a
point t between a and b such that t is
not in S. Then define the two sets
S and a
point t between a and b such that t is
not in S. Then define the two sets
-
U = ( -
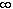 , t ) and
V = ( t,
, t ) and
V = ( t, 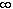 )
)
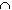 S # 0
(because it contains { a }) and
V
S # 0
(because it contains { a }) and
V 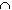 S # 0
(because it contains { b }), and clearly
(U
S # 0
(because it contains { b }), and clearly
(U 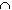 S)
S)
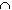 (V
(V 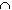 S) = 0.
Finally, because t is not contained in S, we know
that
(U
S) = 0.
Finally, because t is not contained in S, we know
that
(U 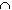 S)
S)
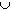 (V
(V 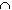 S) = S.
Hence, we have found the required sets U and V to
disconnect S. So, we have proved that if a set is not an
interval it is disconnected. That is equivalent to saying that if it
is connected, it must be an interval.
S) = S.
Hence, we have found the required sets U and V to
disconnect S. So, we have proved that if a set is not an
interval it is disconnected. That is equivalent to saying that if it
is connected, it must be an interval.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of