Theorem 4.2.11: p Series
The series
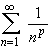 is called a p Series.
is called a p Series.
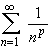 is called a p Series.
is called a p Series.
- if p > 1 the p-series converges
- if p
 1 the p-series diverges
1 the p-series diverges
| Examples 4.2.12: | |
| |
If p < 0 then the sequence
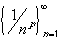 converges to infinity. Hence, the series diverges by the
Divergence Test.
converges to infinity. Hence, the series diverges by the
Divergence Test.
If p > 0 then consider the series
The right hand series is now a Geometric Series.=
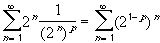
- if 0 < p
 1 then
2 1-p
1 then
2 1-p  1,
hence the right-hand series diverges
1,
hence the right-hand series diverges
- if 1 < p then 2 1-p < 1, hence the right-hand series converges
Now the result follows from the Cauchy Condensation test .
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 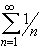 converge or
diverge ?
converge or
diverge ?
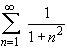 converge or diverge ?
converge or diverge ?
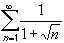 converge or diverge ?
(This is the same series as in the example for the
converge or diverge ?
(This is the same series as in the example for the