Interactive Real Analysis
- part of Examples 4.2.12(a):
The series 
diverges.
Back
diverges.
BackThis series is called harmonic series, and is a p-series with p = 1. Hence, by the p-series test, the series diverges. One can also proof divergence of this series directly by looking at the limit of partial sums.
An interesting application of the harmonic series is the story about the Leaning Tower of Lire.
Note that in contrast to the divergent harmonic series, the alternating
harmonic series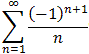 
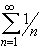converges.