Examples 2.2.2:
Show that all of the following sets are uncountable:
Recall that the set (0, 1) is uncountable, as proved before. Then:
- The open interval (-1, 1) is uncountable
- Any open interval (a, b) is uncountable
- The set of all real numbers R is uncountable
1. Define the function
- f(x) = 2x - 1 from (0, 1) to (-1, 1)
2. A similar proof can show that any open interval (a, b) is uncountable. What is the appropriate bijection (try a linear function that maps 0 to a and 1 to b) ?
3. Define a function
- f(x) =
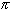 x -
x -
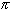 / 2
/ 2
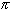 / 2,
/ 2, 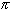 / 2).
Next, take the function
/ 2).
Next, take the function
- g(x) = tan(x)
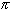 / 2,
/ 2,
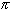 / 2) and R. But then the
composition of the two function will be a bijection from (0, 1) to R,
and hence both sets must have the same cardinality.
/ 2) and R. But then the
composition of the two function will be a bijection from (0, 1) to R,
and hence both sets must have the same cardinality.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of