Examples 2.1.7(c):
Let P be the set of all polynomials with integer coefficients, and define the set P(n) to be the set of all polynomials with integer coefficients and degree n. From before we already know that P(n) is countable. ButHence, P is the countable union of countable sets, and must therefore be countable itself by our result on countable unions of countable sets.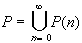
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of