Example 2.3.5(b):

Suppose the induction principle defined above does not contain the assumption that every element except for the smallest has an immediate predecessor. Then show that it could be proved that every natural number must be even (which is, of course, not true so the additional assumption on the induction principle is necessary).
Back

In other words, we assume that the induction principles was stated as follows:

Let S be a well-ordered set Then: if Q is a property such that:
1. the smallest element of S has the property Q
2. if s 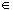S has property Q then the successor of s also has property Q
Then the property Q holds for every element in S

If this principle was true, we could prove that every natural number must be even as follows:

Consider the natural numbers with the ordering << defined as follows:

if n and m are both even, then define n << m if n < m
if n and m are both odd, then define n << m if n < m
if n is even and m is odd, we always define n << m

We have already proved that this set is well-ordered. We want to show that every number is even. Therefore:

Q is the property that every element is even.

The smallest element of our set in the << ordering is 2, which is even.

Also, if s has property Q then so does the successor of s. That is because in our ordering, the successor of an even number is always the next even number, never an odd number, and if s has property Q, then s must be even.

Therefore, by the incorrect induction principle, every natural number is even - which is, of course, not true.

The actual induction principle as we have defined it does, however, not apply to this example, since 1 does not have an immediate predecessor.

This example was suggested by Karl Hahn who pointed out that there is another principle, called Transfinite Induction which - suitably stated - does apply to every well-ordered set. He also suggested the book Set Theory and Logic by Stoll, published by Dover, for further reference on this and other set theoretical topics.

Interactive Real Analysis, ver. 1.9.5
(c) 1994-2007, Bert G. Wachsmuth
Page last modified: Mar 26, 2007