Examples 2.2.8:
We want to add or subtract the following cardinal numbers:
- card(N) + card(N) = card(N)
- card(N) - card(N) = undefined
- card(R) + card(N) = card(R)
- card(R) + card(R) = card(R)
1. card(N) + card(N) = card(N)
According to the definition, this is the same as the cardinality of A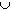 B, where
A and B are both countable, disjoint sets . But the
countable union of countable sets is again countable. Hence,
card(A
B, where
A and B are both countable, disjoint sets . But the
countable union of countable sets is again countable. Hence,
card(A 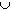 B) = card(N),
so that
B) = card(N),
so that
- card(N) + card(N) = card(N)
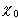 = aleph null = card(N))
= aleph null = card(N))
-
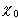 +
+
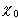 =
=
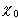
2. card(N) - card(N) = undefined
Although this has not been properly defined, one could say that this should be the same as the cardinality of A \ B, where A and B are both countable sets and B is a subset of A. This creates problems, however, as the following examples show:- A = B = N. Then card(A \ B) = card(0) = 0
- A = all integers, B = even integers. Then card(A \ B) = card(odd integers) = card(N)
- card(N) - card(N) is undefined.
-
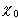 -
-
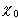 is undefined
is undefined
3. card(R) + card(N) = card(R)
According to the definition, this is the same as the cardinality of A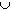 B, where A is
uncountable and B is countable and A and B are disjoint.
We know that every subset of a countable set is countable or finite.
Since A is a subset of
A
B, where A is
uncountable and B is countable and A and B are disjoint.
We know that every subset of a countable set is countable or finite.
Since A is a subset of
A 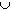 B, the set
A
B, the set
A 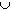 B can not be countable.
Hence, it must be uncountable. We would therefore guess that
B can not be countable.
Hence, it must be uncountable. We would therefore guess that
- card(R) + card(N) = card(R)
- c +
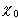 = c
= c
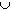 B can not be strictly
larger that the cardinality of A to establish this. That, however, is
left as an exercise.
B can not be strictly
larger that the cardinality of A to establish this. That, however, is
left as an exercise.
4. card(R) + card(R) = card(R)
This should be the same as the cardinality of A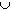 B, where both
A and B are uncountable and disjoint. It is easy to find a
one-to-one function from A to
A
B, where both
A and B are uncountable and disjoint. It is easy to find a
one-to-one function from A to
A 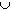 B, so that
card(A)
B, so that
card(A)  card(A
card(A 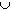 B).
But then card(A
B).
But then card(A 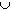 B)
is again uncountable, so that we would guess that
B)
is again uncountable, so that we would guess that
- card(R) + card(R) = card(R)
- c + c = c
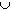 B)
B)
 card(A)
This is true, and left as an exercise.
card(A)
This is true, and left as an exercise.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of