Interactive Real Analysis
- part of 9.5. Cantor, Georg (1845-1918)
Georg Cantor put forth the modern theory on infinite sets that
revolutionized almost every mathematics field. However, his new
ideas also created many dissenters and made him one of the most
assailed mathematicians in history.
Georg Ferdinand Ludwig Philipp Cantor was born in St. Petersburg, Russia, on March 3, 1845. Georg's background was very diverse. His father was a Danish Jewish merchant that had converted to Protestantism while his mother was a Danish Roman Catholic. The family stayed in Russia for eleven years until the father's ailing health forced them to move to the more acceptable environment of Frankfurt, Germany, the country Georg would call home for the rest of his life.
All the Cantor children displayed an early artistic talent with Georg excelling in mathematics. His father, the eternal pragmatic, saw this gift and tried to push his son into the more profitable but less challenging field of engineering. In one of his letters, he pressed upon his son that his entire family and God Himself were expecting him to become a "shining star" as an engineer. Georg was not at all happy about this idea but he lacked the assertiveness to stand up to his father and relented. However, after several years of training, he became so fed up with the idea that he mustered up the courage to beg his father to become a mathematician. Finally, just before entering college, his father let Georg study mathematics. The son accepted his decision with the same submission that he had before, thanking his father for the fact that he would not "displease him."
In 1862, Georg Cantor entered the University of Zurich only to transfer the next year to the University of Berlin after his father's death. At Berlin he studied mathematics, philosophy and physics. There he studied under some of the greatest mathematicians of the day including Kronecker and Weierstrass. After receiving his doctorate in 1867, he was unable to find good employment and was forced to accept a position as an unpaid lecturer and later as an assistant professor at the backwater University of Halle. In 1874, he married and eventually had six children.
It was in that same year of 1874 that Cantor published his first
paper on the theory of sets. While studying a problem in analysis,
he had dug deeply into its "foundations," especially
sets and infinite sets. What he found flabbergasted him so much
that he wrote to a friend: "I see it but I don't believe
it.". In a series of papers from 1874 to 1897, he was able
to prove among other things that the set of integers had an equal
number of members as the set of even numbers, squares, cubes,
and roots to equations; that the number of points in a line segment
is equal to the number of points in an infinite line, a plane
and all mathematical space; and that the number of transcendental
numbers, values such as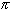 
and e
that can never be the solution to any algebraic equation, were
much larger than the number of integers. Interestingly, the Jesuits
also used his theory to "prove" the existence of God
and the Holy Trinity. However, Cantor, who was also an excellent
theologian, quickly distanced himself away from such "proofs."
Before in mathematics, infinity had been a taboo subject. Previously, Gauss had stated that infinity should only be used as "a way of speaking" and not as a mathematical value. Most mathematicians followed his advice and stayed away. However, Cantor would not leave it alone. He considered infinite sets not as merely going on forever but as completed entities, that is having an actual though infinite number of members. He called these actual infinite numbers transfinite numbers. By considering the infinite sets with a transfinite number of members, Cantor was able to come up his amazing discoveries. For his work, he was promoted to full professorship in 1879.
However, his new ideas also gained him numerous enemies. Many mathematicians just would not accept his groundbreaking ideas that shattered their safe world of mathematics. One great mathematician, Henri Poincare expressed his disapproval, stating that Cantor's set theory would be considered by future generations as "a disease from which one has recovered." However, he was kinder than another critic, Leopold Kronecker. Kronecker was a firm believer that the only numbers were integers and that negatives, fractions, imaginary and especially irrational numbers had no business in mathematics. He simply could not handle "actual infinity." Using his prestige as a professor at the University of Berlin, he did all he could to suppress Cantor's ideas and ruin his life. Among other things, he delayed or suppressed completely Cantor's and his followers' publications, raged both written and verbal personal attacks against him, belittled his ideas in front of his students and blocked Cantor's life ambition of gaining a position at the prestigious University of Berlin.
Not all mathematicians were antagonistic to Cantor's ideas. Some greats such as Mittag-Leffler, Karl Weierstrass, and long-time friend Richard Dedekind supported his ideas and attacked Kronecker's actions. However, it was not enough. Like with his father before, Cantor simply could not handle it. Stuck in a third-rate institution, stripped of well-deserved recognition for his work and under constant attack by Kronecker, he suffered the first of many nervous breakdowns in 1884. The rest of his life was spent in and out of mental institutions and his work nearly ceased completely. Much too late for him to really enjoy it, his theory finally began to gain recognition by the turn of the century. In 1904, he was awarded a medal by the Royal Society of London and was made a member of both the London Mathematical Society and the Society of Sciences in Gottingen. He died in a mental institution on January 6, 1918.
Today, Cantor's work is widely accepted by the mathematical community. His theory on infinite sets reset the foundation of nearly every mathematical field and brought mathematics to its modern form. In addition, his work has helped to explain Zeno's paradoxes that plagued mathematics for 2500 years. However, his theory also has led to many new questions, especially about set theory, that should keep mathematicians busy for centuries.
For related information on Cantor, see: Karl Weierstrass , Zeno of Elea , Cantor function, Cantor set , Cantor-Bernstein theorem , Zeno's paradoxes.
.
Sources
- Bell, E.T. Men of Mathematics. New York: Simon and Schuster, Inc., 1937.
- Muir, Jane. Of Men and Numbers. New York: Dodd, Mead & Company, 1962.
- Wilson, John H. "Cantor." Encyclopedia of World Biography. New York: McGraw-Hill, Inc., 1973. vol. 2, pp. 356-357.