Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Theorem 8.2.3: Uniform Convergence preserves Continuity

If a sequence of functions fn(x) defined on D converges uniformly to a function f(x), and if each fn(x) is continuous on D, then the limit function f(x) is also continuous on D.

All ingredients will be needed, that fn converges uniformly and that each fn is continuous. We want to prove that f is continuous on D. Thus, we need to pick an x0 and show that

|f(x0) - f(x)| < if |x0 - x| <

Let's start with an arbitrary > 0. Because of uniform convergence we can find an N such that

|fn(x) - f(x)| < /3 if n N

for all x 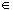D. Because all fn are continuous, we can find in particular a > 0 such that

|fN(x0) - fN(x)| < /3 if |x0 - x| <

But then we have:

|f(x0) - f(x)| |f(x0) - fN(x0)| + |fN(x0) - fN(x)| + |fN(x) - f(x)|
     /3 + /3 + /3 =

as long as |x0 - x| < . But that means that f is continuous at x0.

Next | Previous | Glossary | Map | Discussion