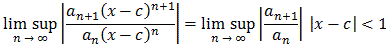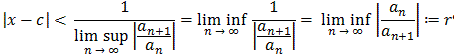Theorem 8.3.7: Power Series
Every power series
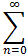 an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
 (i.e. the series converges for all
x).
(i.e. the series converges for all
x).
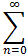 an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
- The power series converges at its center, i.e. for x = c
- There exists an r such that the series converges
absolutely and uniformly for all
|x - c|
 p, where
p < r, and diverges for all |x - c| > r.
The number r is called the radius of convergence for the
power series and is given by:
p, where
p < r, and diverges for all |x - c| > r.
The number r is called the radius of convergence for the
power series and is given by:
r = lim inf | an / an+1|
 (i.e. the series converges for all
x).
(i.e. the series converges for all
x).
This theorem is sometimes called Abel's theorem on Power Series.
Clearly the power series converges for x = c since then all terms except the first reduce to zero. For the second statement, we will simply apply the Ratio test for series:
The series
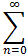 an (x - c)n
converges absolutely if:
an (x - c)n
converges absolutely if:
But then, taking the reciprocal:
which proves that the series converges absolutely for |x - c| < r. The fact that it converges uniformly on any closed disk centered at c with radius p < r follows from the Weierstrass Convergence theorem.

 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of