Proposition 8.1.6: Pointwise Convergence defines Function
There isn't much to prove. We know that since fn converges pointwise, it converges for each fixed x to a limit L(x). The function defined via
f(x) = L(x)
is indeed a function because ... well, because ... let's see, to be a true function we would have for each x exactly one f(x) = L(x). But that must be true by some elementary property of numeric sequences.
Which one?

 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 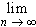 fn(x) = f(x)
is a well-defined function.
fn(x) = f(x)
is a well-defined function.