Definition 8.3.1: Function Series
Suppose { fn(x) } is a sequence of functions and we
define the N-th partial sum as
 D, we denote the
resulting limit function by
D, we denote the
resulting limit function by
SN(x) =Let D be the set of points for which the sequence of partial sums converges pointwise. Then, for xfn(x)
 D, we denote the
resulting limit function by
D, we denote the
resulting limit function by
fn(x) =
SN(x) =
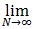
fn(x)
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of