Example 8.3.6 (b): Power Series Examples
Write the following series in sigma-notation and list the general term
an:
- 1 + 2x + 3x2 + 4x3 + ...
- 1 - 1/2 x + 1/4 x2 - 1/8 x3 + 1/16 x4 ...
- 3/2 x + 4/6 x2 + 5/24 x3 + 6/120 x4 + ...
Here we need to determine the general term an so that we can rewrite the series in sigma notation as:
an (x - c)n = a0 + a1(x-c) + a2(x-c)2 + ...
- For 1 + 2x + 3x2 + 4x3 + ... we have:
a0 = 1,
a1 = 2,
a2 = 3,
a3 = 4, ...
so that an = (n+1) and1 + 2x + 3x2 + 4x3 + ... =
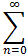 (n+1) xn
(n+1) xn
- For 1 - 1/2 x + 1/4 x2 - 1/8 x3 + 1/16 x4 ... we have:
a0 = 1,
a1 = -1/2 = -1/21,
a2 = 1/4 = 1/22,
a3 = -1/8 = -1/23, ...
so that an = (-1)n 1/2n and1 - 1/2 x + 1/4 x2 - 1/8 x3 + 1/16 x4 ... =
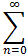 (-1)n 1/2n xn
(-1)n 1/2n xn
- For 3/2 x + 4/6 x2 + 5/24 x3 + 6/120 x4 + ... we have:
a0 = 0 (careful),
a1 = 3/2,
a2 = 4/6 = 4/3!,
a3 = 5/24 = 5/4!,
a4 = 6/120 = 6/5!, ...
so that an = (n+2)/(n+1)! and3/2 x + 4/6 x2 + 5/24 x3 + 6/120 x4 + ... =
Note that the summation this time starts at n=1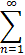 (n+2)/(n+1)! xn
(n+2)/(n+1)! xn
For each series c = 0.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of