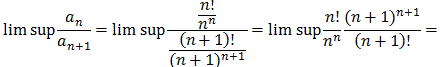Example 8.3.8 (e): Power Series?
The first series has center c = -3 and general term an = n!. Therefore the radius of convergence is:
r = lim sup | an / an+1| = lim sup n!/(n+1)! = lim sup n!/(n+1) n! = lim sup 1/n+1 = 0
That means the series only converges for x = -3, for no other x.
The second series has center c = 4 and general term an = n!/nn. Therefore the radius of convergence is:
r = lim sup | an / an+1| =
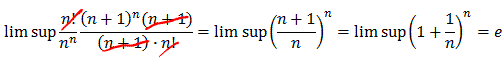
where we used our result on Euler's sequence. That means the series converges for |x - 4| < e. To be picky we need to investigate convergence at the endpoints 'manually', which is left to the reader (sorry).
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 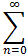 n! (x + 3)n
n! (x + 3)n