Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Example 8.3.12 (d): Differentiating and Integrating Power Series

Find, with proof, a power series centered at c = 0 for the function f(x) = 1/(1-x)2, for -1 < x < 1.

We need to resort to information we already know. We did discuss the geometric series:

1/1-x = xn

Differentiating both sides finishes the problem:

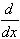
f(x) = 1/(1-x)2 = 1/1-x = xn = nxn-1
n xn-1 f(x) = 1/(1-x)2
Next | Previous | Glossary | Map | Discussion