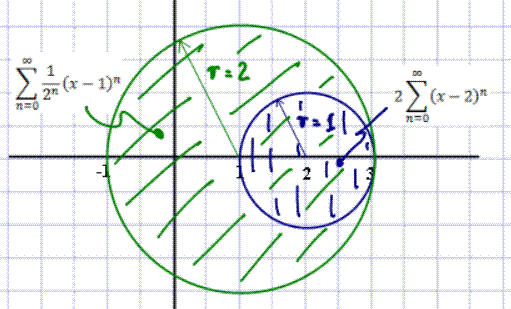
Example 8.3.9 (b): Power Series Center
The power series
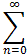 2-n(x-1)n
has center c = 1 and radius of convergence r = 2
(confirm). Re-center the series at c = 2. What is the new
radius of convergence?
2-n(x-1)n
has center c = 1 and radius of convergence r = 2
(confirm). Re-center the series at c = 2. What is the new
radius of convergence?
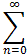 2-n(x-1)n
has center c = 1 and radius of convergence r = 2
(confirm). Re-center the series at c = 2. What is the new
radius of convergence?
2-n(x-1)n
has center c = 1 and radius of convergence r = 2
(confirm). Re-center the series at c = 2. What is the new
radius of convergence?
To solve this, we'll make a slight detour: we know that
xn = 1/1-x
is our familiar geometric series. Substituting x = (t-1)/2 on both sides we get:
2-n(t-1)n = 1/1-(t-1)/2 = 2/3-t
Therefore we have a simple expression (on the right) for our original series (on the left). To center something at c=2 we need to get t-2 involved somehow. Thus:
2-n(t-1)n = 2/3-t = 2/3-(t-2+2) = 2/1-(t-2) = 2
(t-2)n
The center of this series is, as requested, c = 2 and the radius of convergence is r = 1 (as is easily confirmed). Geometrically, the regions of convergence overlap as shown below:
As you can see, inside the blue circle we have two power series representations. Of course they should give the same value, as you can confirm in special cases:
- Let x = 2:
2-n(x-1)n =
2-n(2-1)n =
2-n(1)n =
(1/2)n = 1/1-1/2 = 2
- 2
(x-2)n = 2
(2-2)n = 2 * 1 = 2
- Let x=3/2:
2-n(x-1)n =
2-n(3/2-1)n =
2-n(1/2)n =
(1/4)n = 1/1-1/4 = 4/3
- 2
(x-2)n = 2
(3/2-2)n = 2
(-1/2)n = 2 1/1+1/2 = 2 * 2/3 = 4/3
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of