Interactive Real Analysis - part of MathCS.org

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 8.1. Pointwise Convergence
• 8.2. Uniform Convergence
• 8.3. Series and Power Series
• 8.4. Taylor Series
• 8.5. Approximation Theory
• 9. Historical Tidbits
• Java Tools

Example 8.1.8 (c): Pointwise Convergence does not preserve Integrability

Why these ads ...

Find a pointwise convergent sequence of Riemann-integrable functions whose limit is not Riemann-integrable.

Back

Let r_n be the (countable) set of rational numbers inside the interval [0, 1], ordered in some way, and define the functions

and

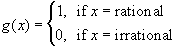
Then:

• The sequence g_n converges pointwise to g
• Each g_n has only finitely many points of discontinuity, thus each g_n is Riemann integrable
• The limit function g is not Riemann integrable

Thus, pointwise convergence does not preserve Riemann-integrability.