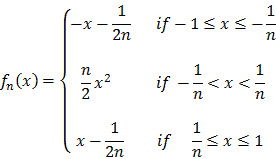Interactive Real Analysis - part of MathCS.org

Next | Previous | Glossary | Map | Discussion

Example 8.1.8 (b): Pointwise Convergence does not preserve Differentiability

Find a pointwise convergent sequence of differentiable functions such that the limit function is continuous but not differentiable.

We first need a function that is continuous but not differentiable. Then we will try to find a sequence of differentiable functions that converge to it.

Our prime example of a non-differentiable, continuous function is, of course, the absolute value function f(x) = |x|. To approximate it by differentiable functions we need to "smooth out" the "kink" at x = 0, for example with a piece of a parabola. In other words, we need a function defined in multiple pieces:

  1. to the left of x=0 the function should look similar to the negative part of the absolute value, i.e. f(x) = -x
  2. to the right of x=0 the function should be close to the positive part of the absolute value, i.e. f(x) = x
  3. in a small neighborhood of x=0 the function should look like a parabola f(x) = a x2 for some positive constant a
  4. of course the function should depend on a parameter n in such a way that:
    • the function is differentiable
    • the function is continuous
    • the function is 'close' to |x|

Let's decide that the 'small neighborhood' mentioned in part 3 is the interval (-1/n, 1/n), inside which the function is a parabola. To ensure its derivative matches up with the derivatives outside that interval, we need f'(x) = 2a x = 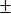1 when x 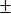1/n. Thus, a = n/2. Finally we need to patch our function to make it continuous at x 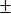1/n. Our finished product is:

You should verify that this function has all of the desired properties:

  • fn(x) is continuous at 1/n and in fact in [-1, 1]
  • fn(x) is differentiable at 1/n and in fact in [-1, 1]
  • fn(x) converges to f(x)=|x|
Next | Previous | Glossary | Map | Discussion