Example 8.1.8 (a): Pointwise Convergence does not preserve Continuity
Find a pointwise convergent sequence of functions, each of which is
continuous, but whose limit function is not continuous.
|
Let fn(x) = xn for
0 Then:
Thus, pointwise convergence does not preserve continuity. |
|
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of  [0, 1] and define
[0, 1] and define
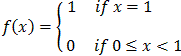
 f
pointwise
f
pointwise