Theorem 8.2.11: Uniform Convergence and Differentiation
Let fn(x) be continuously differentiable functions
defined on the interval [a, b]. If:
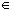 [a, b]. In other
words, the limit process and the differentiation process can be switched in
this case.
[a, b]. In other
words, the limit process and the differentiation process can be switched in
this case.
Then f is differentiable and
- the sequence fn converges pointwise to a function f, and
- the sequence of derivatives fn' converges uniformly
f'(x) =for all xfn'(x)
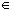 [a, b]. In other
words, the limit process and the differentiation process can be switched in
this case.
[a, b]. In other
words, the limit process and the differentiation process can be switched in
this case.
We already saw that neither pointwise nor uniform convergence by themselves were sufficient to switch limits and differentiation. But together things will work out, as we will see.
The sequence of derivatives fn' converges uniformly and each fn' is continuous. Thus the function defined as:
g(x) =fn'
is well defined and continuous. We also have by the fundamental theorem of calculus that:
fn(x) - fn(a) =fn' (x) dx
By a previous theorem we know that:
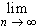
fn' (t) dt =
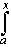
fn' (t) dt =
g(t) dt
But then, together with the previous line, we get:
because the fn's converge pointwise to the function f. Thus:fn(x) - fn(a) = f(x) - f(a) =
g(t) dt
f(x) =g(t) dt + f(a)
But the function on the right, being defined as an integral of a continuous function, is differentiable and therefore f must be differentiable. Indeed, we get that:
f'(x) = g(x) =which is what we wanted to prove.fn'
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of