Theorem 8.2.7: Uniform Convergence and Integration
Let fn(x) be a sequence of continuous functions
defined on the interval [a, b] and assume that
fn converges uniformly to a function f.
Then f is Riemann-integrable and
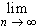
fn(x) dx =
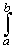
fn(x) dx =
f(x) dx
Since fn are continuous and converge uniformly to f, the limit function must be continuous. In particular all functions must therefore be Riemann integrable. Also:
Since the right side goes to zero as n goes to infinity we are done.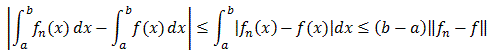
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of