Illustrating Uniform Continuity:
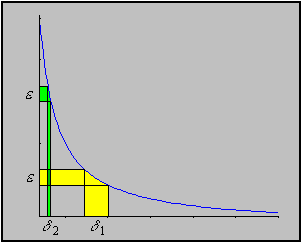
For uniform continuity, there has to be one single
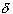 that works for a
fixed, given
that works for a
fixed, given
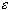 .
In the picture below that is
not possible. If the
.
In the picture below that is
not possible. If the
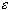 'slides' up the positive
y-axis, the corresponding
'slides' up the positive
y-axis, the corresponding
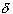 must get smaller and smaller. There
is no single
must get smaller and smaller. There
is no single
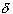 that will work for any possible
location of the
that will work for any possible
location of the
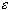 interval on the y axis.
interval on the y axis.
 Not uniformly continuous
Not uniformly continuous
In the example below, however, one can see that regardless of where I
place the
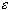 -interval on the y-axis, it is
possible to find one single small
-interval on the y-axis, it is
possible to find one single small
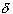 that will work for each of those
locations of
that will work for each of those
locations of
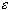 . That is to say, there is one
. That is to say, there is one
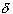 that will work uniformly for all
locations of
that will work uniformly for all
locations of
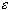 (of course, choosing a smaller
(of course, choosing a smaller
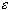 means that I am also allowed to pick
another, smaller
means that I am also allowed to pick
another, smaller
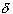 - that will work again uniformly for
all
- that will work again uniformly for
all 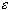 -locations).
-locations).
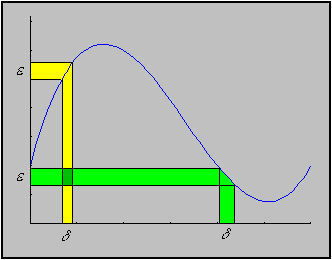 Is uniformly continuous
Is uniformly continuous
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of