Examples 4.2.14(a):
To apply the root test, we have to checklim supby our result on the limit of the n-th root sequence. Hence, the root test, applied to the above series, is inconclusive.= lim sup 1 /
= 1
However, since this series is the harmonic series, we can prove either directly that it diverges or apply the p-series test to show divergence.
Note that the root test also does not apply to the alternating harmonic series, which turns out to converge conditionally.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of 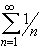 ,
but the series diverges.
,
but the series diverges.