Examples 4.2.6:
Use the limit comparison test together with the results on
p-series to investigate the following series:
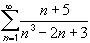
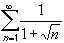
- If r(n) = p(n) / q(n), where p
and q are polynomials in n, can you
find general criteria for the series
 p(n)
to converge or diverge ?
p(n)
to converge or diverge ?
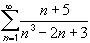
-
Since the term
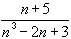 basically looks like
1 / n 2, we want to limit-compare this
series with the p-series
basically looks like
1 / n 2, we want to limit-compare this
series with the p-series
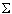 1 / n 2.
In fact:
1 / n 2.
In fact:
Hence, both series have the same convergence behavior, and since the p-series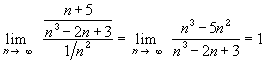
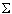 1 / n 2
converges, so does the original series.
1 / n 2
converges, so does the original series.
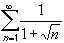
-
Since the term
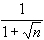 basically looks like
1 /
basically looks like
1 / 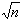 ,
we want to limit-compare with the p-series
,
we want to limit-compare with the p-series
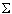 1 /
1 /
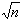 .
In fact:
.
In fact:
Hence, both series have the same convergence behavior, and since the p-series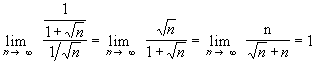
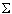 1 /
1 /
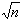 diverges, so does the original series.
diverges, so does the original series.
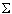 p(n)
p(n)
-
The last series is left as an exercise. Here are some hints:
- The p-series test tells you the convergence
behavior of
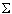 1 /
n k for different k.
1 /
n k for different k.
- Check the limit of an expression like n k r(n) by comparing the degrees of numerator and denominator
- Depending on the answers above, use the limit comparison to find the behavior of the original series, based on the degrees of numerator and denominator.
- The p-series test tells you the convergence
behavior of
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of