Theorem 1.3.3: Equivalence Classes
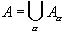 with the following properties:
with the following properties:
- If a,b are in A then a ~ b if and only if a
and b are in the same set
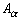
- The subsets
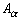 are non-empty and pairwise disjoint.
are non-empty and pairwise disjoint.
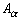 are called
equivalence classes.
are called
equivalence classes.
Proof:
We have to decide what the equivalence classes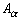 should be: Since by
property (1) two elements a and b are supposed to be related
if and only if they are in the same class, it seems natural to define:
should be: Since by
property (1) two elements a and b are supposed to be related
if and only if they are in the same class, it seems natural to define:
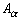 =
{ b
=
{ b 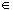 A :
b ~
A :
b ~ 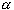 }
}
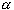 ) . Now we need to check whether
this is a good definition, and whether it satisfies the above properties.
) . Now we need to check whether
this is a good definition, and whether it satisfies the above properties.
Because of reflexivity of the equivalence relation, the class A(a) contains the element a and is therefore not empty.
Next, we will show that two classes that are different can not have any elements in common, i.e. they are disjoint. Recall that disjoint means that two sets have either an empty intersection or are the same sets. Take two elements a and a’ and suppose that A(a) and A(a’) have a non-empty intersection; say both classes contain the element c. Then
- c ~ a, because c is in A(a)
- a ~ c, by symmetry and the above line
- c ~ a’ because c is in A(a’)
- Therefore, by transitivity, a ~ a’
Finally, we need to show that all classes A(a) make up the original set A. But that is clear, because every element a in A belongs to the class A(a), hence the union of all classes A(a) must be contained in A, and therefore must be equal to A.
 Interactive Real Analysis
- part of
Interactive Real Analysis
- part of